Start of topic | Skip to actions
A Stationary Rotating Vortex
We consider a rotating vortex in gaseous flow in two space dimensions. The governing equations are the Euler equations for one polytropic gas. We construct a non-trivial radially symmetric and stationary solution by balancing hydrodynamic pressure and centripetal force per volume element, i.e.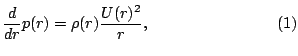
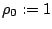 and the velocity field
and the velocity field
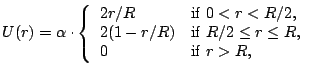 we find by integrating Eq. (1) with boundary condition
we find by integrating Eq. (1) with boundary condition 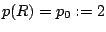 the pressure distribution
the pressure distribution
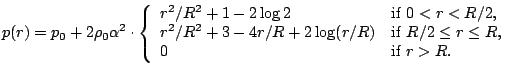 In Cartesian coordinates the entire solution for Euler equations in primitive variables reads
In Cartesian coordinates the entire solution for Euler equations in primitive variables reads
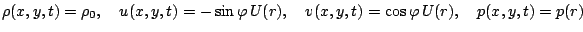
 with
with 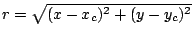 and
and
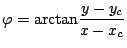 .
This exact smooth solution is applicable to measure the accuracy of Cartesian finite volume schemes alone, but also to quantify the accuracy of imbedded boundary methods by constructing a radially symmetric no-slip boundary around the origin.
Configuration used in accuracy study for available patch solvers:
.
This exact smooth solution is applicable to measure the accuracy of Cartesian finite volume schemes alone, but also to quantify the accuracy of imbedded boundary methods by constructing a radially symmetric no-slip boundary around the origin.
Configuration used in accuracy study for available patch solvers:
![r\in[0,0.5], \quad R=0.4, \quad \alpha=R\pi](http://vtf.website/asc/wiki/pub/Amroc/VortexRotationExactSolution/67c27461b871da65cfd2b99fd427c153.gif)
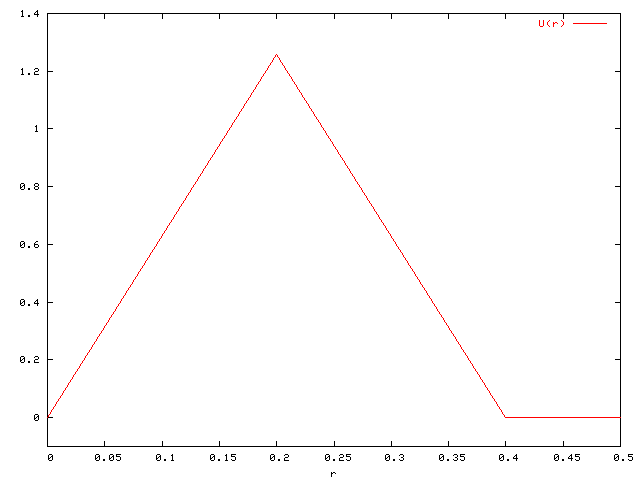 |
| Velocity U(r) |
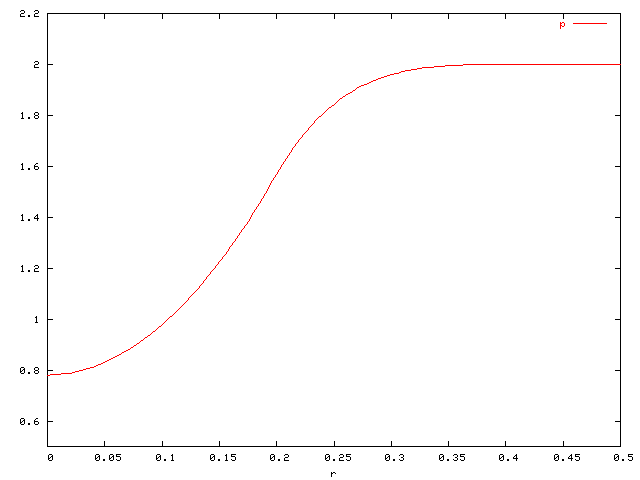 |
| Pressure p(r) |
-- RalfDeiterding - 23 Feb 2005
Copyright © 1997-2025 California Institute of Technology.