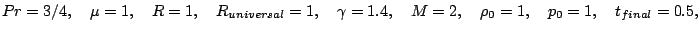Convergence and stability comparison of CLAWPACK and WENO solvers for the 1D Navier-Stokes Equations
We use the exact solution [ViscousShockWave] of a stationary shock wave for the one dimensional Navier-stokes equations as initial conditions and to quantify the error in the convervative variables (density, momentum, and total energy) in the L1 norm. This specific exact solution is available under
ViscousShock in the weno and clawpack: applications/euler/1D directories.
For the following tests we use the computational domain, x = [-30,30], inflow/outflow boundary conditions and the parameters
where the 0 subsript denotes the upstream flow with Mach number two, as used in the non-dimensionalization for the exact solution. The domain is large enough and the final time short enough, to minimize the boundary errors encountered in the resolutions used below.
One-step Clawpack methods
- The one time-step, methods of Clawpack found in Clawpack, have a spatial order of accuracy of first to second order depending on whether or not limiting is used. They are theoretically stable up to CFL=1 for the euler equations. Similarily, for a simple advection-diffusion equation they are theoretically stable up to CFL=1, however, the definition CFL number is changed. For these methods, time step adjustment for CFL=0.99 was used in this 1D viscous, conducting, Navier-Stokes shock example, using a simplified 1d Navier-Stokes model for the CFL number definition. This new CFL number is very robust and stable. This is elaborated upon in [ViscousShockWave].
*Roe solver with
MinMod? Limiting:
Method(1) = 1 (for viscous terms), Method(2) = 2, Method(3) = 0, Limiter(1)= 1, Limiter(2) = 1, Limiter(3) = 1
| N | Roe solver with MinMod? Limiting |
| Density Error | Momentum Error | Total Energy Error | Spatial Order (Component-wise) | Integration Time (sec, one SHC Processor) | time steps | cost/timestep (sec) |
| 1200 | 6.20e-4 | 7.03e-4 | 3.06e-3 | 0.56 | 792 | 7.07e-4 |
| 2400 | 1.56e-4 | 1.77e-4 | 7.74e-4 | 1.99, 1.99, 1.99 | 4.45 | 3090 | 1.44e-3 |
| 4800 | 3.90e-5 | 4.45e-5 | 1.95e-4 | 2.00, 1.99, 1.99 | 36.94 | 12212 | 3.02e-3 |
Three-stage Runge-Kutta WENO methods
- Within the AMROC WENO software, there exist three variants of the WENO method: the classical upwinded order optimized WENO method, Shu[1] and the symmetric WENO method, Candler[2] , which can be order or bandwidth optimized. The symmetric method uses one extra ENO stencil than the classical upwinded WENO method.
- On this Wiki page, when the formal order of accuracy of a pure WENO method (without TCD)is discussed, this is in reference to the order of accuracy that the convective terms are approximated, in a purely hyperbolic problem. For example, this formal order of accuracy can be realized in a smooth Euler equation simuluation. In the current Clawpack and WENO implementation in AMROC, when modeling the full Navier-Stokes equations, 2nd order centered difference stencils are used on the viscous and heat conduction terms and therefore, the order of accuracy of the combined convective and diffusive terms cannot be higher than 2nd order.
- Note: when Method = 0 is used in the solver.in file, as determined by the current Init.f90 file in the weno/src/generic directory, when using the option Order = 2 or 3 the exact same WENO stencil and overall method is used (5-point stencil), and similarily when using the the option Order = 4 or 5, the 7-point stencil is used. This does not occur if Method = 1 is specified. In this case, the stencil size depends on both the specification of the "Order" and "Optimize" options.
- In practice, one can use an order optimized WENO method (Optimize = 0) or a bandwidth optimized WENO method (Optimize = 1). (For the current version of AMROC this option has been disabled Only the symmetric bandwidth optimized WENO method can be used without modifying the source code. The source code was locally modified for the order optimized WENO results on this Wiki page.)
- The bandwidth optimization option is tuned specifically for turbulence and LES problems. In these cases it is advantageous to lower the magnitude (rather than the order) of the error by using WENO weights that are optimized in a spectral sense using fourier analysis. The use of the bandwidth optimized WENO method for applications outside of pure turbulence modeling is unknown.
- Also, note that for the same order of accuracy, the bandwidth optimized WENO method will have a larger overall stencil than the classical order optimized WENO method.
- In all the following charts, UseViscous? = 1 and DoFixup? =1 where specified. Also, cles_dcflag_none1d.f was used.
- For all WENO WENO-TCD solver methods a time step adjustment for CFL=0.6 was used.
| N | WENO - Third Order upwinded order optimized, Method = 0, Optimize = 0, Order = 3, GhostCells = 3 |
| Density Error | Momentum Error | Total Energy Error | Spatial Order (Component-wise) | Integration Time (sec, one SHC Processor) | time steps | cost/timestep (sec) |
| 1200 | 9.47e-5 | 1.63e-4 | 4.84e-4 | 9.14 | 671 | 1.36e-2 |
| 2400 | 2.51e-5 | 3.62e-5 | 1.25e-4 | 1.94, 2.12, 1.97 | 73.48 | 2671 | 2.75e-2 |
| 4800 | 6.15e-6 | 8.75e-6 | 3.05e-5 | 2.02, 2.03, 2.02 | 614.37 | 10671 | 5.75e-2 |
| N | WENO - Fifth Order upwinded order optimized, Method = 0, Optimize = 0, Order = 5, , GhostCells = 4 |
| Density Error | Momentum Error | Total Energy Error | Spatial Order (Component-wise) | Integration Time (sec, one SHC Processor) | time steps | cost/timestep (sec) |
| 1200 | 9.49e-5 | 1.38e-4 | 4.71e-4 | 12.11 | 671 | 1.80e-2 |
| 2400 | 2.37e-5 | 3.45e-5 | 1.18e-4 | 2.00, 2.00, 2.00 | 97.36 | 2671 | 3.64e-2 |
| 4800 | 5.93e-6 | 8.63e-6 | 2.94e-5 | 2.00, 2.00, 2.00 | 802.59 | 10671 | 7.52e-2 |
| N | WENO - Second Order Symmetric bandwidth optimized, Method = 0, Optimize = 1, Order = 3, GhostCells = 3 |
| Density Error | Momentum Error | Total Energy Error | Spatial Order (Component-wise) | Whole Time (sec, one Processor) | time steps | cost/timestep (sec) |
| 1200 | 1.93e-4 | 3.32e-4 | 9.83e-4 | 9.28 | 671 | 1.38e-2 |
| 2400 | 5.50e-5 | 8.20e-5 | 2.74e-4 | 1.87, 2.01, 1.89 | 74.85 | 2671 | 2.80e-2 |
| 4800 | 1.41e-5 | 2.06e-5 | 7.00e-5 | 1.98, 2.00, 1.98 | 622.94 | 10671 | 5.84e-2 |
| N | WENO - Third Order Symmetric bandwidth optimized, Method = 0, Optimize = 1, Order = 5, , GhostCells = 4 |
| Density Error | Momentum Error | Total Energy Error | Spatial Order (Component-wise) | Integration Time (sec, one Processor) | time steps | cost/timestep (sec) |
| 1200 | 9.59e-5 | 1.39e-4 | 4.76e-4 | 12.29 | 671 | 1.38e-2 |
| 2400 | 2.38e-5 | 3.46e-5 | 1.18e-4 | 2.007, 2.004, 2.008 | 98.92 | 2671 | 3.70e-2 |
| 4800 | 5.93e-6 | 8.64e-6 | 2.94 -5 | 2.00, 2.00, 2.00 | 816.96 | 10671 | 7.66e-2 |
- Note that when using Method = 0, the Optimize = 0 or 1 option, in the current version of AMROC, has no effect on how the current WENO implementation runs. With Method = 0, only the classical order optimized WENO methods (3rd and 5th order overall methods) are available. The 3rd order method uses a weighted combination of two 2nd order ENO stencils, and the 5th order method uses a weighted combination of three third order ENO stencils. Also note that the overall 3rd and 5th orders of accuracy, are only realized in numerically smooth flow which has a grid with high resolution. The overall order is 2*EnoOrder-1 for classical order optimized WENO methods only.
Three-stage Runge-Kutta TCD methods
- To use the TCD (tuned centered difference) method, Method = 1 is specified. If cles_dcflag_none1d.f is used (specified in the src/Makefile.am file), then TCD is used everywhere in the simulation. To use WENO and TCD in a hybridized manner, a dcflag (discontuity flag) function must be specified.
- Within the AMROC WENO software, there exist two variants of TCD: the order optimized stencil and the bandwidth optimized stencil.
- When using Method = 1 and Optimize = 1, only bandwidth optimized 2nd and 4th order TCD (tuned centered difference), WENO, and hybrid WENO-TCD is available. Therefore, Order = 2 or 4 is used. Note that in this case, the "Order" parameter corresponds to the bandwidth optimized versions of WENO and TCD.
- When using Method = 1, and Optimize = 0, only order optimized 2nd, 4th, and 6th order TCD stencils is available. Therefore, Order = 2, 4, or 6 is used. In this case, the "Order" parameter corresponds to the order optimized version of TCD. In the current version of the CODE there is no option for using an order optimized WENO method with TCD. Only the symmetric bandwidth optimized WENO method is made available for a Hybrid WENO-TCD method. Therefore, for the Method = 1 and Optimize = 0 case, order optimized TCD is used with bandwidth optimized WENO.
- In all the following charts, UseViscous? = 1 and DoFixup? =1 where specified. Also, cles_dcflag_none1d.f was used.
- For all WENO WENO-TCD solver methods a time step adjustment for CFL=0.6 was used.
| N | TCD - Second Order, Method = 1, Optimize = 0, Order = 2, , GhostCells = 3, cles_dcflag_none1d.f was used |
| Density Error | Momentum Error | Total Energy Error | Spatial Order (Component-wise) | Integration Time (sec, one SHC Processor) | time steps | cost/timestep (sec) |
| 1200 | 8.23e-5 | 1.14e-4 | 5.48e-4 | 1.45 | 668 | 2.17e-3 |
| 2400 | 2.06-5 | 2.85e-5 | 1.37e-4 | 2.00, 2.00, 2.00 | 12.87 | 2668 | 4.82e-3 |
| 4800 | 5.16e-6 | 7.12e-6 | 3.42e-5 | 2.00, 2.00, 2.00 | 129.09 | 10668 | 1.21e-2 |
| N | TCD - Second Order, Method = 1, Optimize = 1, Order = 2, , GhostCells = 3, cles_dcflag_none1d.f was used |
| Density Error | Momentum Error | Total Energy Error | Spatial Order (Component-wise) | Integration Time (sec, one Processor) | time steps | cost/timestep (sec) |
| 1200 | 3.35e-4 | 4.77e-4 | 1.77e-3 | 1.56 | 671 | 2.32e-3 |
| 2400 | 8.40e-5 | 1.20e-4 | 4.44e-4 | 2.00, 1.99, 2.00 | 13.91 | 2671 | 5.21e-3 |
| 4800 | 2.10e-5 | 2.99e-5 | 1.11e-4 | 2.00,2.00 ,2.00 | 137.87 | 10671 | 1.29e-2 |
[1] Chi-Wang Shu. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. Technical Report ICASE Report No. 97-65, Institute for Computer Applications in Science and Engineering NASA Langley Research Center, 1997.
[2] V. G. Weirs and G. V. Candler. Optimization of weighted eno schemes for dns of compressible turbulence. AIAA, 97-1940:1–11, 1997.