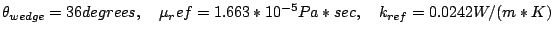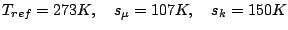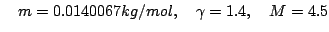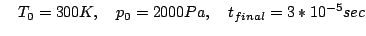Temperature dependent viscosity and conductivity Problem Setup
A temperature dependent viscosity and conductivity model with slip and noslip boundary conditions was tested using the Sutherland model for perfect (constant specific heat) nitrogen. Again, as in the constant viscosity and conductivity model, the Clawpack and WENO methods were compared. The main difference of this test is the significant increase of the diffusive effects behind the Mach stem and around the shear/mixing layer. The viscosity and conductivity increase close to linearly with temperature, and the highest temperatures are between the Mach stem and the shear/mixing layer (aka the slipline in inviscid theory).
- New Parameters for Nitrogen:
24 Processors, SHC
- For the following tests we used the computational domain: x = [-0.01,0.1], y = [0, 0.025]
- Clawpack: base level 220x50 cells with levels refined 2,2,4,4 times respectively, max cfl = 0.9
- WENO-TCD: base level 220x50 cells with levels refined 2,2,2,4 times respectively, max cfl = 0.85
64 Processors, SHC
- For the following tests we used the computational domain: x = [-0.01,0.1], y = [0, 0.025]
- 5 levels: base level 110x25 cells with 4 more levels refined 2,2,4,4 times respectively
DoubleMachReflectionStudy
--
JackZiegler? - 11 Aug 2008