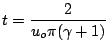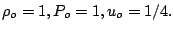Start of topic | Skip to actions
Riemann (1860) presented a solution to the one-dimensional Euler equations in which the velocity and pressure
are functions of density only. Landau in Section 101 gives the explict relations for a simple wave in a polytropic gas assuming
that there is a point in the wave for which v =0
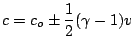
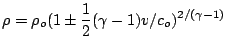
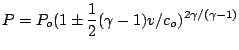 ..
with the velocity defined implicity by
..
with the velocity defined implicity by
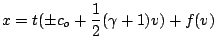 or alternately
or alternately
![v=F[x-(\pm c_o + \frac{1}{2}(\gamma +1)v)t]](http://vtf.website/asc/wiki/pub/Amroc/SimpleWave/248238e0d25fd1892ff490916be68010.gif) A Fortran90 code that computes this exact solution using a Newton-Raphson method has been written and maybe found in the repository. The velocity spectra of the exact solution is also
computed (using an FFT).
While the code may be easily modified, it currently assumes that the initial velocity profile is a single mode of the form
A Fortran90 code that computes this exact solution using a Newton-Raphson method has been written and maybe found in the repository. The velocity spectra of the exact solution is also
computed (using an FFT).
While the code may be easily modified, it currently assumes that the initial velocity profile is a single mode of the form
![F[x,t=0] = u_o \sin[\pi x].](http://vtf.website/asc/wiki/pub/Amroc/SimpleWave/a9f63e30d0bff91034589e2229450cfe.gif) For such an initial condition it can be shown that the shock develops at the time
For such an initial condition it can be shown that the shock develops at the time
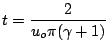 An example simple wave an .avi animation shows the density up to breaking as computed by the exact solution, while a simulation using the TCD-WENO scheme computes past breaking. The parameters
for this example were
An example simple wave an .avi animation shows the density up to breaking as computed by the exact solution, while a simulation using the TCD-WENO scheme computes past breaking. The parameters
for this example were 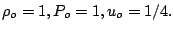 This exact solution with the is used to study the convergance of the skew-symetric form of the solver in the Simple Wave Simulations section.
-- DavidHill - 20 Dec 2004
This exact solution with the is used to study the convergance of the skew-symetric form of the solver in the Simple Wave Simulations section.
-- DavidHill - 20 Dec 2004
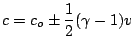
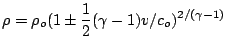
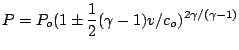
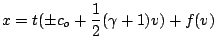
![v=F[x-(\pm c_o + \frac{1}{2}(\gamma +1)v)t]](http://vtf.website/asc/wiki/pub/Amroc/SimpleWave/248238e0d25fd1892ff490916be68010.gif)
![F[x,t=0] = u_o \sin[\pi x].](http://vtf.website/asc/wiki/pub/Amroc/SimpleWave/a9f63e30d0bff91034589e2229450cfe.gif)