Print preview

Numerical Simulations of Gaseous Detonations

Detonations with One-Step Chemistry

Normalization

Under the assumption of a planar stationary detonation wave propagating with constant speed d the inhomogeneous Euler equations can be solved exactly. These planar one-dimensional solutions are used as initial conditions for all simulations with the one-step model.

Further on, all following computations for the one-step reaction model utilize dimensionless quantities. With

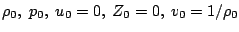
$\rho_0,\; p_0,\; u_0=0,\; Z_0=0,\; v_0=1/\rho_0$

denoting the values in the unburned gas and

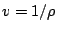
$v=1/\rho$

the employed normalization reads

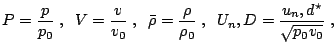
$P = \frac{p}{p_0}\;, \;\; V = \frac{v}{v_0}\;, \;\; \bar{\rho} = \frac{\rho}{\rho_0}\;, \;\; U_n,D = \frac{u_n,d^\star}{\sqrt{p_0 v_0}}\;,$

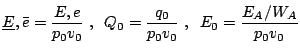
$\underline{E},\bar e = \frac{E,e}{p_0 v_0}\;, \;\; Q_0 = \frac{q_0}{p_0 v_0}\;, \;\; E_0 = \frac{E_A/W_A}{p_0 v_0}$

and

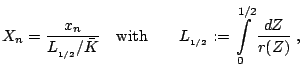
$X_n=\frac{x_n}{L_{_{1/2}}/\bar K} \quad {\rm with} \qquad L_{_{1/2}}:=\int\limits_{0}^{1/2} \frac{dZ}{r(Z)}\;,$

where

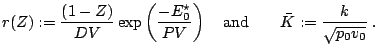
$r(Z) := \frac{(1-Z)}{DV}\exp \left(\frac{-E_0^\star}{PV}\right) \quad {\rm and}\qquad \bar K:=\frac{k}{\sqrt{p_0 v_0}} \;.$

-- RalfDeiterding - 14 Dec 2004

End of topic
Skip to action links | Back to top

You are here: Amroc > ClawpackHome > NumSimGasDet > DetonationsOneStepChemistry > OneStepNormalization

to top