Start of topic | Skip to actions
Proximal Bodies in Hypersonic Flow
Problem Description
In this problem, we seek to determine the forces experienced by a secondary body in the shocked region created by a primary body travelling at hypersonic speeds. The problem is considered in two and three dimensions - in the first case bodies are circular cylinders; in the second, spheres. The flow is created by a ramping up of flow speed at the left boundary to a freestream Mach number of 10. The downstream displacement of the secondary body is fixed (at 4 and 3 primary body radii, center-to-center, for the cylindrical and spherical cases respectively), while the axial displacement is varied. These computations are to be compared to a series of experiments in the T5 Hypervelocity Shock Facility. [source codes]- Configuration for the spherical case:
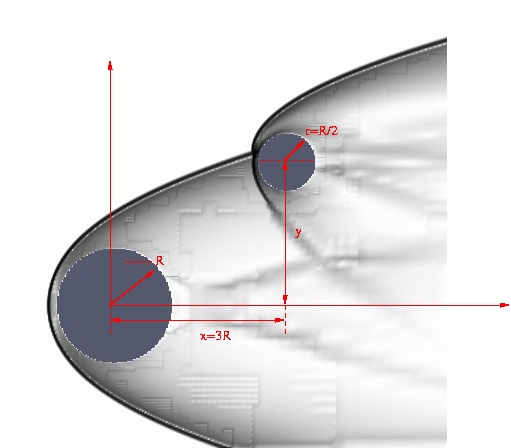
Numerical Simulation
- Euler equations in two- and three-dimensions, using an ideal gas (air with
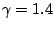 )
)
- Van-Leer flux vector splitting with Godunov dimensional splitting
3-D
- AMR-computation with coarse grid of 40x40x32; up to four additional refinement levels, each with refinement factor 2
- approximately 1400 timesteps with CFL-No. 0.8 to t=3 (approx. 1200 timesteps to t=2.5 for computation with 4 additional refinement levels)
- computational domain 1.25x1.25x1; sphere radii 0.16 and 0.08 respectively
- Timing information ...
Results
- Force coefficients on second body as a function of axial displacement for simulations with 3 additional refinement levels:
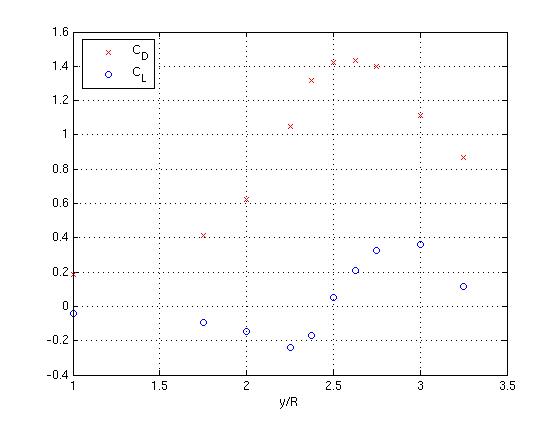
- Drag coefficient on first sphere:

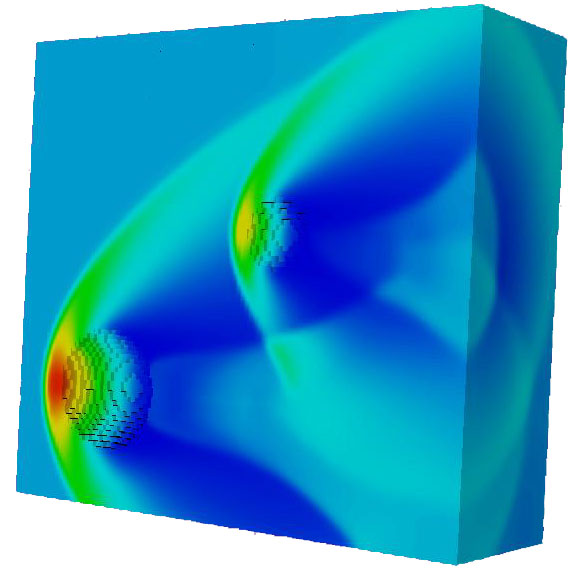
- Color plot of pressure distribution in 3D:
Refinement study
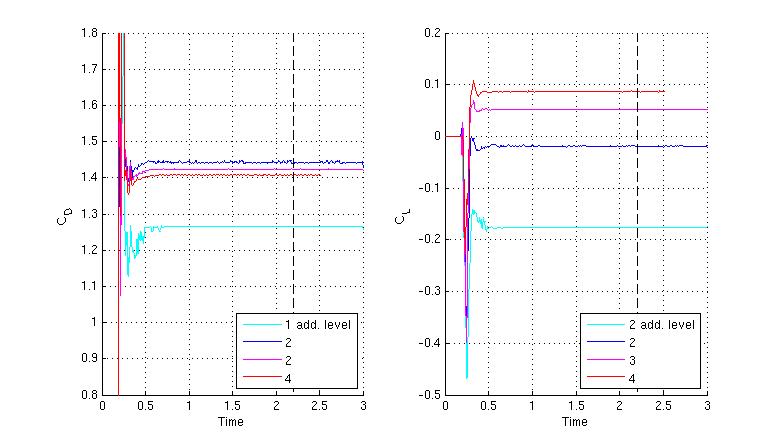
A refinement study has been carried out, in which the axial displacement of the secondary body is 2.5 primary body radii. Values for the drag and lift coefficients of the second body for different levels of refinement are given in the accompanying table. The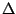 value is the difference between the current level value and that from the previous level. The attached figure shows the time histories of the drag and lift profiles. The dashed vertical line indicates the point after which the time averages are taken.
value is the difference between the current level value and that from the previous level. The attached figure shows the time histories of the drag and lift profiles. The dashed vertical line indicates the point after which the time averages are taken.
| Additional levels | 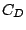 | 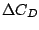 | 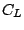 | 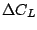 |
| 1 | 1.264 | -0.176 | ||
| 2 | 1.442 | 0.178 | -0.019 | 0.157 |
| 3 | 1.423 | -0.019 | 0.052 | 0.071 |
| 4 | 1.408 | -0.015 | 0.087 | 0.035 |

-- StuartLaurence - 23 Jan 2005
| I | Attachment  | Size | Date | Who | Comment |
|---|---|---|---|---|---|
| | spheres_drag.mpg | 1021.5 K | 02 Feb 2005 - 06:02 | StuartLaurence | Movie of flow startup with force histories on the two spheres |
| | stable_schlieren.mpg | 4937.7 K | 04 Mar 2005 - 17:29 | StuartLaurence | Schlieren movie of stable flow over two cylinders |
| | schlieren_3d.mpg | 808.4 K | 04 Mar 2005 - 21:51 | StuartLaurence | Computational schlieren movie of startup process over two spheres |
| | unstable_schlieren.mpg | 8743.3 K | 10 Mar 2005 - 00:29 | StuartLaurence | Schlieren movie of unstable flow over two cylinders |
| | stability_comparison.mpg | 16295.4 K | 10 Mar 2005 - 01:25 | StuartLaurence | Movie of schlieren superimposed on refinement level sets showing stable and unstable flow development |