Accuracy Study for Ghost-fluid Method
We use the exact solution of a stationary rotating vortex for 2D Euler equations as initial conditions and to quantify the error in the density in the L1 norm. This specific exact solution is available under
VortexRotationExactSolution. The computational codes are available here:
[Clawpack],
[WENO]
For the following tests we use the computational domain [0,1]x[0.1] and the parameters
The ghost fluid boundary is a circle around
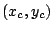
with radius
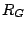
and rotates by itself with velocity
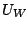
.
We access the accuracy of the Ghost-fluid method implemented generically in AMROC for the
- truly second-order multi-dimensional Wave Propagation Method with Roe solver and 2 imbedded ghost cells used, CFL=0.9,
- first-order Godunov-splitting with Roe solver and 2 imbedded ghost cells used, CFL=0.9,
- pure WENO-7 Pt and 3 imbedded ghost cells used, CFL=0.6.
- The entire density loss throughout the calculation because of the non-conservative boundary is measured.
Consistency test - boundary rotation in uniform flow
In order to test, if the imbedded boundary method is able to reproduce a uniform flow field in a non-trivial boundary situation, we use
For Euler equations zero flow should be introduced and first order unstructured schemes that use a
consistent numerical flux at the imbedded boundary, i.e. that default to the exact flux function, can be shown to preserve constant flow for all time steps.
First test with reflecting slip wall boundary conditions at the imbedded boundary:
| N | Wave Propagation | Godunov-Splitting | WENO - 7 Pt |
| Error | Order | Mass loss | Error | Order | Mass loss | Error | Order | Mass loss |
| 20 | 1.729e-05 | | -9.136e-07 | 3.718e-05 | | -7.567e-07 | 3.232e-05 | | 6.297e-06 |
| 40 | 1.646e-05 | 0.07 | -5.025e-08 | 1.736e-05 | 1.10 | -3.570e-08 | 2.024e-05 | 0.68 | -2.086e-08 |
| 80 | 5.595e-06 | 1.56 | -2.383e-09 | 5.702e-06 | 1.61 | -1.190e-09 | 5.919e-06 | 1.77 | -3.122e-10 |
| 160 | 1.472e-06 | 1.93 | -1.343e-10 | 1.399e-06 | 2.03 | -9.116e-11 | | | |
Second test with extrapolation boundary conditions at the imbedded boundary:
| N | Wave Propagation | Godunov-Splitting | WENO - 7 Pt |
| Error | Order | Mass loss | Error | Order | Mass loss | Error | Order | Mass loss |
| 20 | 5.970e-05 | | -8.862e-07 | 4.491e-05 | | -1.105e-06 | 0.0001210 | | 5.108e-05 |
| 40 | 2.571e-05 | 1.22 | -4.916e-08 | 1.766e-05 | 1.35 | -4.630e-08 | 1.574e-05 | 2.94 | -4.361e-08 |
| 80 | 3.316e-06 | 2.95 | -2.402e-09 | 3.697e-06 | 2.26 | -2.103e-09 | 4.358e-06 | 1.85 | -1.821e-09 |
| 160 | 1.168e-06 | 1.51 | -1.359e-10 | 1.176e-06 | 1.65 | -1.098e-10 | | | |
- As the error arises only at the boundary, the accuracy of the imbedded boundary dominates the measured error. The accuracy of the underlying scheme becomes negligible.
- The error is non-uniform along the boundary as the GFM boundary conditions are not invariant to rotation. A movie with the temporal development of the magnitude of the velocity vector (Wave Propagation) clearly shows this.
-
Shear flow test 1 - negligible flow along imbedded boundary
In order to test the imbedded boundary method for a situation with hardly any boundary interaction we use
Imbedded boundary conditions: reflecting slip wall.
| N | Wave Propagation | Godunov-Splitting | WENO - 7 Pt |
| Error | Order | Mass loss | Error | Order | Mass loss | Error | Order | Mass loss |
| 20 | 0.0120056 | | 0.0079236 | 0.0144203 | | 0.0020241 | 0.0064736 | | 0.0028641 |
| 40 | 0.0035074 | 1.78 | 0.0011898 | 0.0073070 | 0.98 | 0.0001300 | 0.0017008 | 1.93 | 0.0004790 |
| 80 | 0.0014193 | 1.31 | 0.0001588 | 0.0038401 | 0.93 | -0.0001036 | 0.0006816 | 1.32 | -5.878e-05 |
| 160 | 0.0005032 | 1.50 | 5.046e-05 | 0.0018988 | 1.02 | -2.783e-06 | | | |
- As the dependency of the solution on the imbedded boundary is negligible all methods show their unperturbed order of accuracy as in VortexRotationAccuracyStudy.
Shear flow test 2 - strong flow along imbedded boundary
In order to test the imbedded boundary method for a situation with very strong shear flow we place the imbedded boundary exactly at point of maximal shear flow veclocity, i.e.
First test with reflecting slip wall boundary conditions at the imbedded boundary:
| N | Wave Propagation | Godunov-Splitting | WENO - 7 Pt |
| Error | Order | Mass loss | Error | Order | Mass loss | Error | Order | Mass loss |
| 20 | 0.0423925 | | 0.0423925 | 0.0271446 | | 0.0271446 | 0.0260747 | | 0.0260747 |
| 40 | 0.0358735 | 0.24 | 0.0358735 | 0.0242260 | 0.16 | 0.0242260 | 0.0236603 | 0.14 | 0.0236603 |
| 80 | 0.0212340 | 0.76 | 0.0212340 | 0.0128638 | 0.91 | 0.0128638 | 0.0128931 | 0.88 | 0.0128931 |
| 160 | 0.0121089 | 0.81 | 0.0121089 | 0.0070906 | 0.86 | 0.0070906 | | | |
Second test with extrapolation boundary conditions at the imbedded boundary:
| N | Wave Propagation | Godunov-Splitting | WENO - 7 Pt |
| Error | Order | Mass loss | Error | Order | Mass loss | Error | Order | Mass loss |
| 20 | 0.0575232 | | 0.0575232 | 0.0512302 | | 0.0512302 | 0.0376556 | | 0.0376556 |
| 40 | 0.0479454 | 0.26 | 0.0479454 | 0.0417552 | 0.30 | 0.0417552 | 0.0303673 | 0.31 | 0.0303673 |
| 80 | 0.0327630 | 0.55 | 0.0327630 | 0.0272841 | 0.61 | 0.0272841 | 0.0196045 | 0.63 | 0.0196045 |
| 160 | 0.0206183 | 0.67 | 0.0206183 | 0.0166053 | 0.72 | 0.0166053 | | | |
- The accuracy of the imbedded boundary dominates the measured error. All schemes show the same degradates accuracy.
- Godunov-splitting and WENO-7Pt show a comparable absolute error. Both methods use only fluxes normal to a cell boundary.
- The multi-dimensional Wave Propagation Method shows a larger absolute error, which indicates that a lumped boundary treatment is inappropriate for this scheme.
- The exact solution is not symmetric around R/2. Although the solution has the property
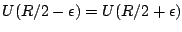 , the pressure is not symmetric, i.e.
, the pressure is not symmetric, i.e. 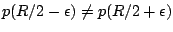 .
.
- Boundary conditions implemented with ghost cells make a significant modelling error.
Conclusions
- Even analytically constructed values in ghost cells are not seen correctly in the multi-dimensional finite volume scheme. (See consistency test).
- Interpolation at points away from the boundary to construct boundary values can be inappropriate to model boundary conditions. (See test for shear flow test 2).
- Lumping of boundary and interpolation diffuse shear flows (See test for shear flow test 2).
- Lumped boundary results in loss of conservation. Under grid refinement this error always declines, but no order measurement seems reasonable.
--
RalfDeiterding - 23 Feb 2005
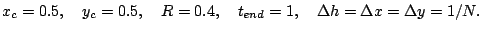
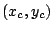 with radius
with radius 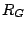 and rotates by itself with velocity
and rotates by itself with velocity 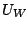 .
We access the accuracy of the Ghost-fluid method implemented generically in AMROC for the
.
We access the accuracy of the Ghost-fluid method implemented generically in AMROC for the
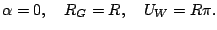

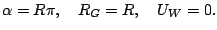
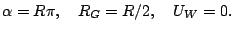
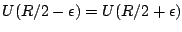 , the pressure is not symmetric, i.e.
, the pressure is not symmetric, i.e. 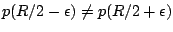 .
.