Design of AMROC's DAGH
AMROC is formulated on top of a heavily modified version of the DAGH (Distributed Adaptive Grid Hierarchies) package originally released by Manish Parashar and James C. Browne. The DAGH package stores all data in parallelized hierachical grid functions that follow automatically the "floor-plan" of a single grid hierarchy and capsulates technical parallelization details completely against the adaptive framework. DAGH automatically synchronizes neighbouring subgrids, applies boundary conditions, generates and deletes subgrids, distributes them in a load-balanced manner, etc.
AMROC's version of DAGH implements GridFunction [bad link?]- and GridHierarchy [bad link?]-classes that are much more general and allow a more efficient adaption than those of the original DAGH package. This generality required a complete rewriting of parts of the codes. Various useful features like different refinement factors on each level, multiple periodic boundary conditions, a restart from memory for automatic time-step algorithms based on the CFL-condition and a restart feature for a different number of computing nodes have been added additionally.
The most important elementary classes inside DAGH are the BBox [bad link?]-class. BBox defines a rectangular box in a global integer index space. Methods for geometric operations on boxes like concatenation or intersection are available. GridData adds consecutive data storage to a BBox-object. The geometrical description of all refinement areas is stored in hierarchical GridBoxLists inside GridHierarchy. Several "distributed'' GridFunctions of various storage types create GridDataBlock [bad link?]-objects with a GridData-objects for the raw data according to these lists. The GridHierarchy consists of global GridBoxLists storing the complete refinement information and GridBoxLists for each processor's local contribution. During computation, the grid hierarchy is dynamically repartitioned under the restriction that higher level data must be assigned to the same processor as the coarsest level data. As GridDataBlock-objects are generated directly from these local GridBoxLists, all GridFunctions become equally distributed following the actual "floor plan''. Redistribution over processors is carried out automatically as a natural part of the AMR-algorithm whenever the grid hierarchy changes.
Note that the described data representation model assigns multiple GridDataBlock-objects stored in different GridFunctions to a single subgrid. The AMR-algorithm utilizes rectangular data blocks of various storage type to handle a single refinement grid, but in our design these blocks are accessed via GridDataBlock-objects kept in different GridFunctions.
This special design follows from the perception that the tedious technical overhead in implementing the AMR-method in a distributed memory environment can be simplified significantly, if commonality in organizing rectangular data blocks independent of their storage type is exploited. This common functionality is concentrated inside the GridFunction-class and by employing template data types and compile-time parameters carefully all GridFunction-objects are derived from this base class without a loss of computational performance.
AMR requires hierarchical GridFunctions of various spatial dimensions, with complex storage data types and with differently sized overlap regions. Deriving all GridFunction-objects from one base class guarantees a common interface and most parts of AMROC have been coded independently of spatial dimensions and size of the vector of state.
A change of the hierarchy is initiated by clustering flagged cells into suitable BBoxes. Each processor has to generate a properly nested BBoxList of new refinement regions in his actual contribution of the computational domain. These lists are used to update the global grid hierarchy. A global union of these BBoxLists is constructed on each level. The workload of the entire hierachy is estimated and accumulated in GridUnit-objects. The minimal size of a GridUnit is one cell of the coarsest level. The usage of larger GridUnits can be enforced with GridHierarchy.setgucfactor(), the GridUnit-coarsening factor. The partitioning algorithm called by DAGHDistribution breaks up the derived composite GridUnitList in load-balanced portions and assigns a local GridUnitList to each processor. Each node derives its new local GridBoxList by intersecting its local GridUnitList with the global union of BBoxLists.
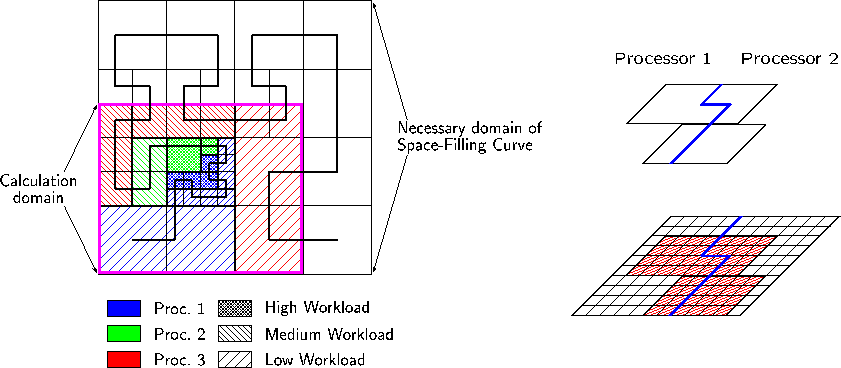
The algorithm used for partitioning the computational domain has to meet several requirements. It must balance the estimated workload, while maintaining patches of sufficient size. The algorithm should be fast, because it is executed after each regrid operation. Additionally, communication for redistributing GridFunctions and synchronizing them during calculation should be minimal. DAGH employs a generalization of the Peano-Hilbert space-filling curve as a partitioner that. It is implemented in the PeanoHilbert-class. Note that the generalized Peano-Hilbert space-filling curve can only be defined on a domain with equal extends on all sides that are a power of 2. Therefore the domain that is internally used for the space-filling curve usually exceed the computational domain (see fig. 4). This is the reason why the space-filling curve can not produce perfectly connected distributions in all cases.
After recomposing GridHierarchy's local GridBoxList all GridFunctions have to be redistributed. It depends on the type of the particular GridFunction how the newly created patches have to be initialized.
Figure 4: Usage of Hilbert's space-filling curve as a partitoner (left). All data of all levels is distributed to the same node (right).
-- RalfDeiterding - 12 Dec 2004