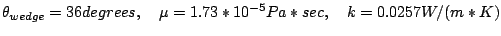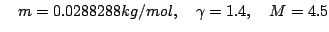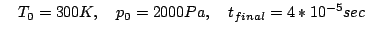DMR GFM Problem Set up
For the following tests we use the computational domain, x = [-0.005,0.07], y = [0, 0.06], Outflow boundary conditions on the right, post shock BC's on the left, and symmetric slip bc's on the bottom left start up region and on the GFM ramp boundary. On the top boundary, outflow BC's were used. Because the shock is perpendicular to this boundary, the errors encountered here are small (unlike the equivalent problem in a rotated frame of reference).
The gas for this test was a Perfect Gas (constant specific heat, viscosity, and conductivity
where the 0 subsript denotes the pre-shock flow (which in the shock stationary frame of reference has a Mach number of 4.5).
- A base level of 150 x 120 cells was used initally for all Clawpack simulations, with 4 levels of refinement (2, 2, 2, 4), with 24 processors on SHC. Note, that this resolution (relative to the physical dimensions of the problem) is exactly the same resolution used in the rotated DMR ramp problem. However, the number of cells in the base grid is twice as large. This is was used because a 150x120 grid is more efficent for parallelization than a 75x60 grid with refinement levels of 2,2,4,4.
- Special Note for WENO-TCD and GFM: For the stability of the WENO-TCD methods, when using as much TCD as possible, the size of the base grid was increased from that of the initial Clawpack simulations with which they would be compared. With a mesh refinement that is too aggressive, the errors encountered in the problem would be magnified and the method would "ring" and become unstable. This difficulty is more apparrent for the 4th order WENO-TCD rather than the 2nd order, and becomes worse with high levels of refinement (for example 4 instead of 2) and when using no WENO on the slip line. For reasons of parallel efficiencey, the base grid was twice refined rather than addding a 6th level of refinement (such that the refinement would be 2,2,2,2,2 rather than 2,2,2,4), which would have also solved the problem.
- These difficulties were not encountered when computing the solution in a rotated frame of reference which allows one to avoid using the GFM boundary condition on the "ramp". In this rotated case, the mach stem at the ramp is more aligned with the cartesian boundary.
DoubleMachReflectionStudy
- 300x240 base grid 2,2,2,2 refinefinement, unless noted