Start of topic | Skip to actions
3D Euler equations - Periodic boundary conditions
3 Grid Levels (density, isosurface at 1.2)
Results: 3 Levels
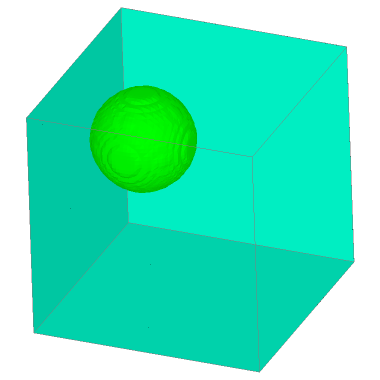 |  | |
| t=0 | t=0.21 |
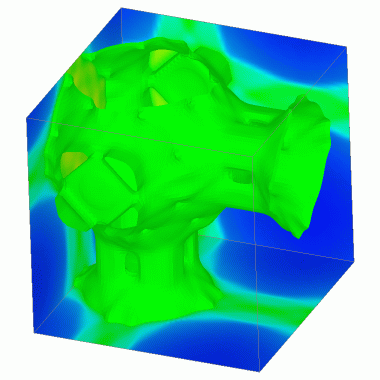 |
| t=0.84 |
Analogue to 2D computation (cuts at z=0.0 and z=0.5)
Benchmark
| Task | P=1 | P=2 | P=4, BufferWidth=2 | P=4, BufferWidth=1 | P=4, Uniform | |||||
| s | % | s | % | s | % | s | % | s | % | |
| Integration | 47865 | 91.6 | 24065 | 78.4 | 12405 | 72.8 | 7363 | 64.9 | 13212 | 97.9 |
| Flux correction | 799 | 1.5 | 1368 | 4.5 | 1116 | 6.6 | 0 | 0.0 | 0 | 0.0 |
| Boundary setting | 530 | 1.0 | 2709 | 8.8 | 1926 | 11.3 | 1720 | 15.2 | 129 | 1.0 |
| Recomposition | 2364 | 4.5 | 2091 | 6.8 | 1326 | 7.8 | 1724 | 15.2 | 0 | 0.0 |
| Clustering | 415 | 0.8 | 225 | 0.7 | 114 | 0.7 | 51 | 0.4 | 0 | 0.0 |
| Misc. | 262 | 0.5 | 222 | 0.8 | 133 | 0.8 | 480 | 4.3 | 148 | 1.2 |
| Total / Parallel Efficiency | 52235 | 100.0 | 30679 | 85.1 | 17021 | 76.7 | 11338 | 115.2 | 13489 | 96.8 |
|---|---|---|---|---|---|---|---|---|---|---|
In this example large regions of the computational domain require adaption. An uniformly refined calculation needs less computational time on four computing nodes (P=4) than an adaptive computation with the usual buffer witdth of two additional cells. If the buffer width is reduced to one cell, the adaptive computation catches up. But, the calculated result becomes incorrect. This example shows drastically that in the general case a buffer width of two cells is unavoidable.
Comparison between the two adaptive and the uniformly refined computation
-- RalfDeiterding - 06 Dec 2004